The System of Profound Knowledge was developed by W. Edwards Deming across a lifetime of improvement work. It provides a map of theory by which to understand the organizations that we work in. The theory has four parts that interact to form the science of improvement: (1) Appreciation for a System, (2) Knowledge about Variation, (3) Theory of Knowledge, and (4) Psychology. 

The aim of this month’s post is to describe the Theory of Knowledge component.

What’s your theory?

How do we improve the math engagement rates discussed in last month’s post? In other words, what would your theory be for improving these rates? 

Don’t get too caught up in the idea of theory. By theory I mean any set of assumptions that you use to predict what’s going to happen in the future. Here, I simply mean the plan or strategy you’d suggest to improve those rates. The plan or strategy you choose is based on the prediction that it will improve the 8th grade math engagement rates, and your underlying rationale for your choice in plan or strategy is your theory. Theory of Knowledge then is the study of how what we think we know and claim to know actually is the way we claim it is.

Rational prediction requires theory. Theory is the basis of all investigation, and the basis for any action we take to attempt to improve systems within our organizations has to include testing our theories. W. Edwards Deming developed a tool called the Plan-Do-Study-Act cycle, or PDSA cycle, for this purpose. A PDSA is a learning cycle that mirrors the scientific method. A prediction (hypothesis) is detailed, data is collected to test the prediction, and the data is analyzed to determine to what extent the prediction was accurate. The accuracy of the prediction is an observable measure of the knowledge we have about the system under study. Given that all attempts to improve educational systems are social and human resource intensive activities, the critical question for PDSA cycles is not “What works?” but rather “What works, for whom, and under what set of conditions?” During the cycle, observed outcomes are compared to predictions and the differences between the two become the learning that drives decisions about next steps with the theory. The knowledge generated through each PDSA cycle ultimately becomes the evidence that some process, tool, or modified staff role or relationship works effectively under a variety of conditions and that quality outcomes will reliably ensue in our system.

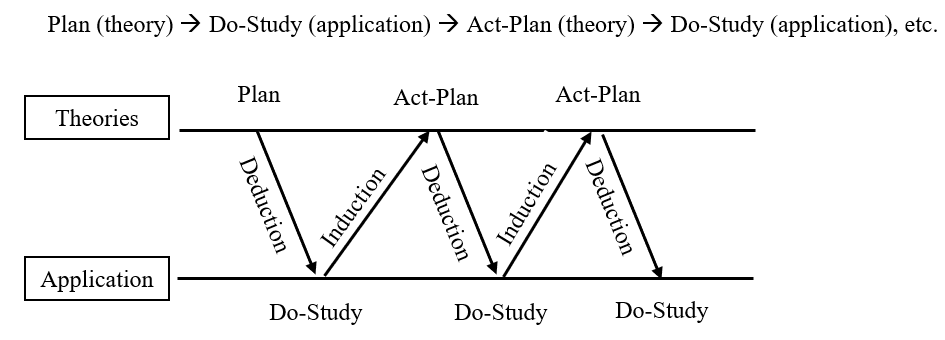
Deductive & Inductive Learning

The foundation of the Plan-Do-Study-Act cycle is the deductive and inductive learning that occurs as you move back and forth between the theory phase of the cycle and the application phase. The iterative nature of the PDSA cycle is illustrated in Figure 1. 

Figure 1. Learning and PDSA

During the cycle, moving from planning to doing is deductive learning and moving from doing to studying is inductive learning. Deductive learning involves moving from a theory to the test of the theory. From Plan to Do is a deductive approach where a theory is tested with the aid of a prediction. In the Do phase, observations are made and differences from the prediction are noted. Inductive learning involves using results from the test to revise the theory. From Do to Study is an inductive approach where gaps or anomalies to the prediction are studied and the theory is updated accordingly. The final step in the PDSA cycle is to Act on the learning from the phase which includes planning the subsequent cycle. 

Enumerative & Analytic Studies

Astute systems leaders reading this post on the Theory of Knowledge, especially those with a Ph.D., may very well be wondering by this point, “Where is the randomized trial?” The randomized controlled trial (RCT) sits atop the research method hierarchy in many fields, including education, and plays an important epistemological role as a mechanism to get at the “truth” about what works in schools. However, while the RCT is likely well-known as a research method amongst educational leaders, what is less appreciated are the limits of the RCT. Deming said that the purpose of any statistical study is to provide a rational basis for taking action, but that the important distinction between the type of study needed for a particular type of improvement centers on where the action will be taken. He classified studies into two categories according to the location of the action taken:

• An enumerative study is a statistical study in which action will be taken on the material within the frame being studied. The aim is estimation about some aspect of the group of items.

• An analytic study is a statistical study in which action will be taken on the process or cause-system that produced the frame being studied, the aim being to improve practice in the future. 

Enumerative studies such as an RCT are not adequate for studying complex, unstable, nonlinear social change.  Rather, these studies are meant to enumerate, that is explain or evaluate, the conditions that exist within the existing population under study while controlling for certain variables during a snapshot in time. On the other hand, analytic studies are focused on improvement of the process which created the results of the past and that will continue creating future results. The domain of continual improvement is almost entirely focused on the ability to predict future performance using analytic studies within the local context, while including the variables for which the RCT controls. 

Knowledge has Temporal Spread

Deming’s conception of the Theory of Knowledge was significantly shaped by Shewhart’s Theory of Variation. The process behavior chart displayed in Figure 1 in last month’s post is an attempt to define the actual present within the process limits. Shewhart used three-sigma, to define the limits; a choice he based on both statistical theory as well as his experience at Bell Labs.  The baseline 8th grade math engagement data provides an approximate range of the possible rates from that system in the future with the acknowledgement that you cannot say for sure if the engagement rates will continue in a similar fashion or if special causes will occur. The engagement data is an example of an analytic study. Action would have to be taken on the 8th grade math causal system to improve performance in the future. 

Like the engagement data, almost all data we are interested in improving in schools occurs across time, and in many cases this chronology is the point. It’s the pattern that emerges from viewing the data in time order that gives us the most insight into what is happening with the data we are analyzing. This is what Deming indicated when he said that knowledge has temporal spread, meaning that our best understanding for how the processes and systems in our organizations are performing can only be interpreted after we view the variation of this data over time. 

In addition to the PDSA, with its cycles of prediction and learning, the concept of operational definitions is another key component of the Theory of Knowledge. Operational definitions put communicable meaning into a concept and include a method of measurement or test as well as a set of criteria for judgment. Concepts that are important to schools such as attendance, engagement, graduation, and learning have no communicable value until they are expressed in operational terms. The learning that comes through PDSA cycles is meaningless in the absence of a shared definition for the concept under study because there is no true value for any measurement in and of itself. 

Theory of Knowledge in Action

Returning again to the 8th grade math engagement example from last month, the importance of operational definitions became readily apparent as schools were shut down due to the pandemic in Spring 2020. Because of the speed with which schools had to transition to remote learning, we quickly learned that although the four schools within United Schools Network were reporting engagement levels, there wasn’t a shared operational definition. There is no true value for this concept until there is a set of criteria to determine when a student has been engaged as well as a method for measuring engagement. 

USN’s two middle schools are located just five miles from each other, but they initially had two very different conceptions of engagement. In one middle school, students had to complete the lesson practice in its entirety to be counted as engaged. In the other middle school, students were counted as engaged if the lesson practice was at least partially completed. By the time the following school year began, both schools had elected to use the more rigorous definition of engagement where students had to complete the practice set that accompanied a lesson in its entirety. With the definition in place, we then were able to turn our attention to building a measurement system that allowed us to assess the capability, stability, and variation within our remote learning system. This example from the transition to remote learning exemplifies the power of operational definitions. They make it possible to share meanings for the concepts that we measure to avoid misunderstandings and conflicts, and ultimately so that we can both communicate during change efforts and have a clear yardstick to tell if these efforts did in fact lead to improvement.

Without theory, there is no way to use the information that streams into our educational systems. The Theory of Knowledge can assist us as systems leaders to accumulate local reports of effectiveness of improvement ideas juxtaposed against sometimes contradictory findings in the literature. This brings us to an important question. What happens when the learning from PDSA cycles suggests one course of action while evidence from more formal methods suggest another? 

Here an analogy may help. If I am a ship’s captain, then general navigation theory will serve me well while crossing the open ocean. However, as I approach the Eastern seaboard of the United States, say near the Port of Baltimore, at the point I enter the port I turn navigation over to the local harbormaster. This is done because the harbormaster has practical knowledge about how to take the ship in and out of this particular port. In the context of the 8th grade math system, the harbormaster is the teacher, the students, and others who are working on the ground in the USN school where the engagement data is being generated. General navigation theory is analogous to the teacher understanding the research-literature on engaging middle school students. This is the knowledge generated by controlled scientific studies. While important, the knowledge generated by the teacher running PDSA experiments with his students to increase remote learning engagement rates is an arguably more important and seldom appreciated component of the organizational improvement process. General navigation theory brings you to the entrance of the port where the local knowledge of the harbormaster becomes of supreme importance. Theory of Knowledge gives us the tools to generate the local knowledge necessary to navigate the port, that is the actual classrooms and schools where we find ourselves daily.

Understanding Profound Knowledge

In this post, I introduced the idea of Theory of Knowledge. I’ll cover the final component of the System of Profound Knowledge, Psychology, in next month’s post.  For additional information on how United Schools Network is applying the ideas discussed in this article, you can check out recent interviews on the Lean Blog Interviews Podcast and on the Connecting the Dots podcast. 

***
John A. Dues is the Chief Learning Officer for United Schools Network, a nonprofit charter management organization that supports four public charter schools in Columbus, Ohio. Send feedback to jdues@unitedschoolsnetwork.org.